隐含赔率(Implied Odds)这个概念理解起来并不难,但许多玩家在实战中会误用它。这会导致一些本可轻易避免却代价高昂的错误,例如追逐一手不值得追的听牌。
为了帮助你避免此类错误,本文将带你学习什么是隐含赔率,以及它应该如何影响你的策略。

一、什么是隐含赔率?
隐含赔率指的是:如果你在后续街次(转牌圈和河牌圈)击中了你的补牌(outs),你预期能从对手那里额外赢得的筹码量。这个概念通常与底池赔率结合使用,来帮助你判断用听牌去跟注是否值得。
如果你预期在击中听牌后能从对手那里赢得更多筹码,那么你就拥有很好的隐含赔率。但如果你预估在后续街次无法从对手那里拿到更多价值,那么你的隐含赔率就很差,甚至没有。
精确计算隐含赔率几乎是不可能的,因为它需要量化和权衡无数个变量——后续街次可能出现的每一张牌、每一种行动、每一种下注大小等等。你最多也只能运用逻辑进行估算。
不过,你可以计算出的是,为了让一个本身无利可图的跟注变得合理,你在后续街次需要赢得的最小金额。这正是我们接下来要讨论的内容。
二、隐含赔率如何运作?
想象一下,在一个盲注1/2的cash局,你在有利位置拿着K♥️Q♥️。转牌圈公共牌面是A♥️6♦️2♠️9♥️——这给了你坚果同花听牌。底池里有20,对手下注15。
快速计算一下底池赔率:15跟注/(20底池+15下注+15跟注)=0.3,表明你需要超过30%的赢率才能有利可图地跟注。由于只有一张牌没发,你击中同花的概率大约是20%,如果不考虑后续行动,你在这里就必须弃牌。
这就是隐含赔率发挥作用的地方。这里有一个公式,可以计算出为了证明你在转牌圈的跟注是合理的,你在河牌圈需要赢得多少:
跟注大小/(底池大小+对手下注大小+你的跟注大小+X)=你的手牌赢率
你可能会注意到,这与底池赔率的公式非常相似。唯一的区别在于分母中增加的“X”和等式右侧你的手牌赢率。
现在,让我们求解“X”:
15/(20+15+15+X)=0.2
15/(50+X)=0.2
15=0.2×(50+X)
15=10+0.2X
5=0.2X
X=25
这意味着,当你用K♥️Q♥️在河牌圈击中同花时,你需要赢得超过25才能使你在转牌圈的跟注变得有利可图。由于届时底池里已经有50,平均来看,你只需要在河牌圈打出一个约等于一半底池的下注并被跟注即可。
这个结果看起来是完全可行的,尤其是在遇到对手也是同花的情况下,还有可能赢得一个巨大的底池。所以,在这手牌中,你应该在转牌圈跟注。
三、隐含赔率运用示例
让我们通过几个例子来把这个概念牢牢印在你的脑海里。坐稳了——接下来的内容会有点复杂。
1.大盲位vs按钮位(翻前跟注,单一加注底池)
假设你在大盲位,是翻前的跟注者,处于不利位置,手持J♦️7♦️。你在翻牌圈跟注了对手的持续下注。
到了转牌圈,牌面是K♦️T♦️3♠️2♥️,你面临来自按钮位玩家的下注,他往67的底池里下注50,他后手还有117的筹码(你的筹码比他多)。
你的底池赔率是:50/(67+50+50)≈0.3=需要30%的赢率才能有利可图地跟注。
下图是你对抗一个相当平衡的连开两枪范围时的赢率(紫色方框部分):
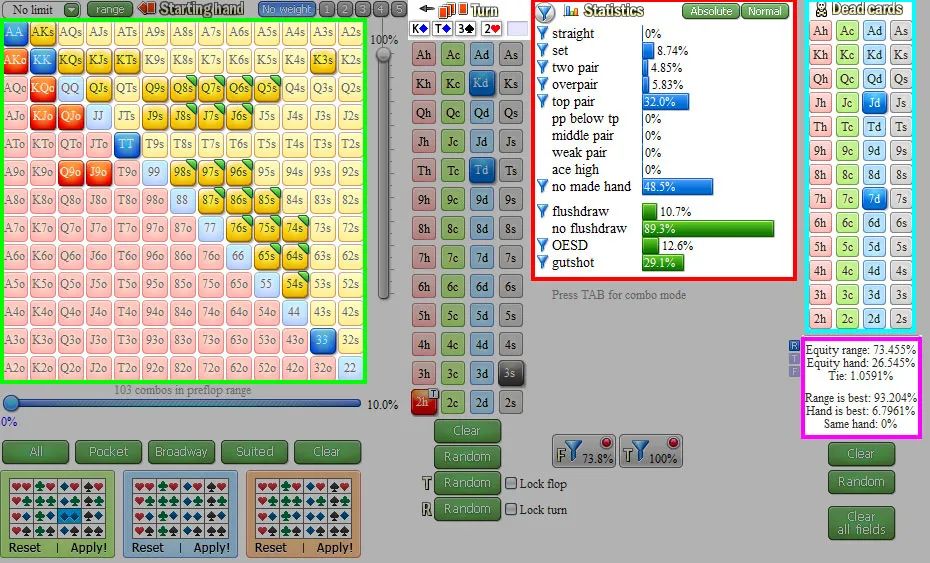
紫色方框=赢率,绿色方框=对手的预估范围,红色方框=范围统计数据(点击可放大)
可以看到,如果我们只考虑底池赔率,我们的赢率是不够的(只有26.5%)。但这是对局势不完整的评估——我们还没有考虑河牌圈会发生什么。
我们有19.6%的概率在河牌圈击中同花——为了方便计算,我们四舍五入到20%。同样,为了简化,我们假设每次在河牌圈击中同花我们都能赢下底池(实际上,我们拿着最好牌的概率约为96%)。
现在,我们用之前的公式来计算,当我们在河牌圈击中听牌时,需要赢多少才能让我们在转牌圈的跟注实现盈亏平衡:
50/(67+50+50+X)=0.2
50/(167+X)=0.2
50=0.20×(167+X)
50=33.4+0.2X
16.6=0.2X
X≈83
我们需要在击中同花后,从按钮位玩家那里赢得83。河牌圈的底池将是167,这意味着我们必须打出一个约等于半个底池的下注并被跟注才能实现盈亏平衡——并且记住,按钮位玩家后手只剩下117了。
由于按钮位玩家在河牌圈不会100%继续下注,尤其是当同花听牌击中时,你需要采取以下行动之一来获取必要的价值:
反主动下注。如果我们选择这个选项,对手的反应必须平均为我们带来83的收益。例如,如果我们反主动下注全下117,按钮位玩家必须至少在70%的情况下跟注。
过牌-跟注(如果他不全下,则过牌-加注)。同样,这需要平均为我们带来83的收益。例如,他需要在至少70%的情况下全下117,我们才能在转牌圈的跟注上实现盈亏平衡。
这些结果是有可能发生的,但都不太可能完全按照我们需要的方式发展。与K♥️Q♥️的例子不同,我们这次击中听牌后拿到的不是坚果牌,我们还处于不利位置,而且对手能让我们赢的筹码也不多了。所有这些原因都使得在河牌圈获取必要的价值变得异常困难。
你可以看到,即使我们将隐含赔率纳入考量,我们仍然无法用这样一手弱听牌进行有利可图的跟注。然而,我们的分析确实表明,这次跟注并不像我们之前想象的那么糟糕。
注意:这里的计算经过简化,排除了一些即使纳入考虑,对结果影响也微乎其微的因素。这些因素包括:在河牌击中J或7并在双方过牌时赢下底池、遇到更大的同花、遇到更小的同花。
2.按钮位vs大盲位(翻前加注,单一加注底池)
隐含赔率并不仅仅用于当你拿着听牌面临下注时。当你是下注者时,它们同样重要。思考以下情况:
你在按钮位率先加注,被大盲位跟注。翻牌是J♣️️️️8♦️5♥️。
当你在构建你的持续下注策略时,可以将手牌的隐含赔率考虑进去。为了说明这一点,我们来看两手可能的牌:J♥️9♥️和A♦️J♠️。
首先是J♥️9♥️。这是一手值得在两条街下注来获取价值的牌,所以问题是我们如何获取最大价值:是应该“翻牌下注-转牌下注-河牌过牌”,还是“翻牌下注-转牌过牌-河牌下注”,或是“翻牌过牌-转牌下注-河牌下注”?
让我们考虑一下当转牌发出9,我们击中两对时的可能情况——这对这手牌来说是一个关键的策略性转牌:
情况1:你持续下注并被跟注。转牌来了张9。现在,对手会认为你的范围更强了,因为像QT、T7s、76s这样的顺子听牌都完成了。这意味着你的两对能获得的价值会变少,并且当对手恰好有QT时,你还会遭受反向隐含赔率的损失。
情况2:你持续下注并被加注。你跟注,转牌又是9。你的对手会非常频繁地在这张牌上开第二枪,因为他的范围(76s以及部分QT、T7s)因这张牌而大幅增强。你被迫跟注,接下来的处境会很艰难。
情况3:你过牌,转牌是9。你的对手现在有大量的潜在诈唬牌,如AT、KT、T6s、T4s、T3s、T2s、KQ、Q7s、Q6s、Q4s、Q3s、Q2s等等。他会用这些牌向你施加巨大压力,因为他的QT、T7s和76s已经完成了,而你恰好拿着一手非常强的牌来跟注他。
从这些情况中你可以看到,用这手牌过牌是最佳选择。当转牌发出那张最容易被对手猛烈攻击的牌时,它因为击中两对而非常好打。
接下来,我们看A♦️J♠️。用这手牌,在某些牌面组合下你能获得三条街的价值,而在另一些情况下只能获得两条街。所以,假设这手牌值2.5条街的价值。我们该如何榨取最大价值呢?
同样,我们专注于那张能让我们组成两对的转牌(一张A),因为这对这手牌来说是关键的策略性转牌:
情况1:你持续下注并被跟注。转牌是A。这张牌对你的范围的提升比对大盲位的更大,这意味着他会更不愿意用像8X和5X这样的牌来跟注你的第二枪。无论如何,你都拥有了一手非常强的牌,而且没有任何听牌完成,你几乎总是可以为了价值连开三枪。
情况2:你持续下注并被加注。你跟注,转牌来了张A。这张牌对你的范围提升比对大盲位的更大,这意味着他会更谨慎地进行诈唬(总体而言)。尽管如此,你的牌现在变得能击败他一部分的价值牌,并且没有任何听牌完成,这意味着你可以轻松跟注。
情况3:你过牌,转牌是A。这张牌极大地增强了你的范围,你的对手会以非常高的频率过牌。因此,你将很难从他的诈唬牌中获得价值。
你可以清楚地看到,为什么在这种情况下用AJ进行持续下注是必须的。所有情况都鼓励我们立即往底池里投入筹码。
结论
隐含赔率不仅在你面临下注时很重要,在你主动下注时也同样重要。
它能帮助你构建防守和进攻范围,如果运用得当,还能对你的赢率产生巨大影响。正确理解隐含赔率将帮助你更频繁地创造出轻松且有利可图的局面。希望本文能帮助你做到这一点。








